台灣風險分析學會

 

 

 2021年第11期

動態系統分岔理論之介紹      

 國立臺灣大學生物環境系統工程學系 胡明哲、劉泰億、張天恩
   Release:July12,2021

 

本文將介紹動態系統(dynamical systems)的風險分析，動態系統描述系統狀態隨著時間或空間的變化，可用來描述物理、生態、環境、農業系統中觀測對象的數量隨時間之動態變動過程。動態系統的風險分析稱為分岔理論（Bifurcation theory），當任一系統（物理系統或自然系統）中的參數(Parameter)持續產生微小的變動，這樣的變動在突破某個臨界點(Critical stage)之後，導致了系統平衡狀態的突然改變，也就是動態系統的平衡解隨不確定性因子的變動，產生分岔現象的過程。

動態系統模型以數學式來描述動態系統則可表示如式(1)，其中x_1,x_2,…,x_n 代表系統中各個狀態變數(state variable)，(x_1 ) ̇,(x_2 ) ̇,…,(x_n ) ̇則為各狀態變數隨時間或空間的變化，式(1)表示各個變數隨時間空間的變化與所有的狀態變數有關。動態系統的不動點是指不隨時間變化的系統穩定狀態，不動點又稱為平衡(Equilibrium)解，意即在該點不會隨著時間或空間而有所變化，不動點為函數映射到其自身一個點，若以數學式表示則如式(2)。

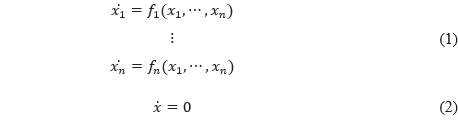
若針對動態系統的不穩定破壞風險進行分析。在上述的動態系統中，假設有一不穩定風險的擾動，根據此不動點對於微小擾動的反應，可將不動點分為穩定(Stable)不動點與不穩定(Unstable)不動點。若在不動點給予微小擾動後，該點仍然可以收斂回原本的不動點，則稱該點為穩定不動點；反之若給予微小擾動後會遠離該不動點，該點則稱為不穩定不動點。通常穩定不動點又稱為attractors或sinks，而不穩定不動點則又稱為repellers或sources。在圖形表示上，穩定不動點常以實心圓表示，不穩定不動點則以空心圓表示。

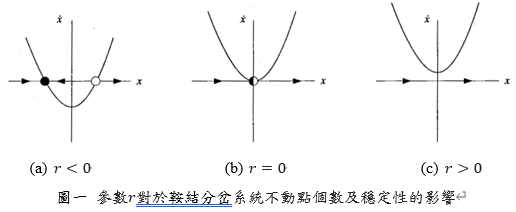
分岔理論用來分析風險動力學的動態系統中，風險動力的系統結構、不動點的穩定性或其他特性參數變化，風險造成的系統變化稱之為穩定狀態的分岔，而產生變化時參數的值即稱為分岔點(Bifurcation points)。分岔理論可以提供整個系統的漸變及穩定性隨著控制參數而變化的資訊。例如常見的鞍結分岔 (Saddle-Node Bifurcation)為系統之不動點產生或消失的機制，在參數改變的過程中，兩個不動點會向彼此逐漸靠近、合併、甚至消失，以下舉例說明。若某系統可以表示成

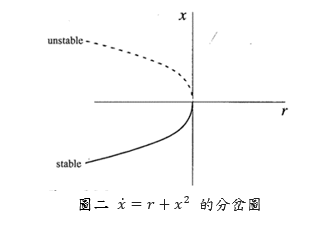
其中r為參數，可為正數、負數或零，當r<0時，整個系統會有兩個不動點，其中一個為穩定，另一個為不穩定，如圖一(a)。然而當r由負數逐漸趨近於0時，圖一中的拋物線會漸漸往上移，造成橫軸上兩個不動點會逐漸向彼此靠近。當r=0時，兩個不動點則合併為一個，此時不動點為x^*=0，且為半穩定狀態，如圖一(b)。而當r>0時，此系統則不存在不動點，如圖一(c)。藉由圖二此類的圖形可得以觀察不動點的特性及整個系統的結構隨著參數改變的變化，這類的圖則稱之為分岔圖(Bifurcation diagram)。

 

 

參考文獻

1. Steven H. Strogatz, Nonlinear Dynamics and Chaos: with Applications to Physics, Biology, Chemistry, And Engineering, ‎1994.

下載PDF檔